4. CONSEQUENCES 2 |
|
Let us sum up the opinions of the physicists of previous generations and, with the use of our theory, let us try to develop a common view to the processes coursed in atom, nucleus and in the Universe.
1. In accordance with Hertz, 1 circulation of electron around nucleus gives us 1 oscillation or 1 wave with a top and a bottom or one elementary quantum of energy respectively, which equals to Planck’s constant.
2. An electron moving at the accelerated speed radiates an electromagnetic wave motion (electrodynamics).
3. An electron moves along the ellipse, with the nucleus in the focus (Bohr’s planetary model).
4. An electron moves at the accelerated speed when approaching the nucleus. When departing, it moves at the decelerated speed (Keppler-Bohr).
5. If an electron moves uniformly along the circle, it does not radiate - series edge.
If the electron moves along the most elongated ellipse, it radiates the series head - there are major changes in acceleration and deceleration.
Other spectral lines of series between these two extremes are the more or less deformed ellipses in dependence on the line thickness.
6. The thicker the line, the more deformed the ellipse.
7. The thinner the line, the more approximate the circle, the orbit of the electron.
8. The invisible "line" represents the motion of electron along the ideal circle. It is the inertial motion.
9. The electron does not move along the same ellipse, but it occurs the coiling of perinucleum i. e. it moves along the rosette in plane (Sommerfeld explained this through equations for the theory of relativity. We explain it through Emov according to equation 2.20). At the same time it is the idea of a "superfine structure" and a "plane quantization".
10. "The space quantization" can be explained according to our theory by means of pushing the center of gravity and the rotating electron getting off the orbit plane, like it is shown in 3.1. - the rotating circle getting off in the gravitation field of the Earth.
11. The radius of force reach of the electron decreases with the increasing translational speed - see relation (3.25). It increases with the decreasing translational speed.
12. The radius of force reach of the electron analogically decreases with the increasing angular (rotating) speed. It increases with the decreasing angle speed of the rotating electron around its axis of revolution.
13. The effective cross-section of oscillating nuclei is decreases with the increase of the particle speed around balanced position of nucleus.
14. The effective cross-section of incident particle decreases with the increase of particle translational speed (e. g. electron, proton) and is inversely proportional to the square of the particle mass.
|
|
15. In the center-of-mass coordinates system
the electron and also the nucleus (of hydrogen atom) revolve at the same
frequency but at different circumferential velocity, whereby it is valid
that ![]()
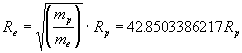
Re - radius of electron revolving
Rp - radius of proton revolving around the common center
of gravity (Currently used equation ![]() see Beiser [9] page 151 is not valid)
see Beiser [9] page 151 is not valid)
16. The relation ![]() results meanwhile also from the law of moment conservation ...
results meanwhile also from the law of moment conservation ... ![]() and the definition and calculation of the moment of inertia
and the definition and calculation of the moment of inertia ![]()
for the sphere ... ![]()
for the cylinder ... ![]() see Steiner’s theorem, too.
see Steiner’s theorem, too.
17. That is why it is also valid (for the hydrogen atom)
![]()
since ![]() ,
,
![]() whereby
the frequency in center-of-mass system is the same for electron as well
as for proton (nucleus).
whereby
the frequency in center-of-mass system is the same for electron as well
as for proton (nucleus).
18. The electron velocity ![]() is at the same time the constant of fine structure whereby according to
Wichman p. 65 (Quantum physics - Berkeley course of physics IV.) and our
theory it is valid that
is at the same time the constant of fine structure whereby according to
Wichman p. 65 (Quantum physics - Berkeley course of physics IV.) and our
theory it is valid that
![]()
Substituting for Tkin according to (3.24) for ![]() we have
we have
![]()
19. The speed of ![]() corresponds to the wavelength of electron
corresponds to the wavelength of electron ![]() ,
one revolvement of which can be coordinated to the Planck’s constant h.
,
one revolvement of which can be coordinated to the Planck’s constant h.
20. Alternately, acceleratively
and deceleratively moving electron at the speed from vmin=0.0029970729c
to vmax=0.0030012425c (8.9975 . 105m/s)
i. e. the electron moves along the rosette radiating electromagnetic wave
(and absorbing energy during deceleration) it will not fell down on the
nucleus as Beiser affirms [9] p. 132. In any case,
the electron moving alternately acceleratively and deceleratively along
the rose orbit of the rosette radiate the electromagnetic wave. If we picture
a concrete most deformed ellipse belonging mainly to the head of Balmer’s
series ![]() as a rosette in the circular ring of the radii of
as a rosette in the circular ring of the radii of ![]() ,
as the circle of the radius of 31cm of the line thickness of 0,3 mm, then
the whole rosette is pressed into this "circle" i. e. into the
circle ring of the thickness of 0,3 mm!
,
as the circle of the radius of 31cm of the line thickness of 0,3 mm, then
the whole rosette is pressed into this "circle" i. e. into the
circle ring of the thickness of 0,3 mm!
We therefore draw the entire circle ring, it seems outwardly, that it is the motion along the circle (ideal one) - only at the depth view to the circle thickness ("through microscope") we can see that in fact it is the rosette - the system of coiling ellipses.
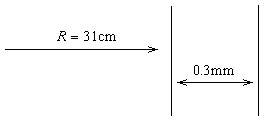
21. Superfluidity
The lower temperature, the lower frequency of revolution of electrons
(protons). At the absolute zero ![]() .
.
As the temperature decreases, the revolvement of the electron and the nucleus around the common center of gravity are impeded. The rotation of electron around its axis nearly stops as well first. The orbital motion stops first, this allowed by the rotational stop.
Conversely: If we start to warm up the electrons and nucleus from the absolute zero, the rotational motion will increase first (the superfluid component HeII.) and only if this rotational motion is saturated to a certain degree, it will also start increasing the orbital motion (as it is in the case of the rotating circle in the gravitational field of the Earth - the electron begins its getting off the nucleus). Therefore the normal component HeII contains also the orbital motion of electron. The superfluid component (=not containing friction) would be characterized only by the rotating electrons around their axes in HeII atoms, whereby the motion along the orbit does not yet begin (our it could be very slow respectively).
The normal component would be also characterized by the motion of electrons along the orbits around the nuclei (more exactly, around the centers of gravity of atoms). But this normal component contains friction like the result of the revolution of electrons and protons along the orbits around the center of gravity of atom.
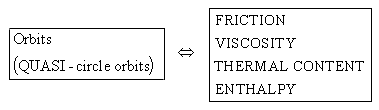
All these quantities (friction, viscosity,...) start up only with the
registration of the orbital motion beginning as the result of high accelerated
rotation around its axis ![]() .
.
The superfluid state is exactly the state, in which the mass is least willing to express its properties.

During the rotation we get two circular paraboloids, the big one of
height h is normal component HeII and a smaller one under the big one of
height ![]() in the superfluid component representing the mixture of rotating electrons
and nuclei around their own axis.
in the superfluid component representing the mixture of rotating electrons
and nuclei around their own axis.
The thermal content is made dependent upon the exclusive existence of the atom electron envelope.
| If I have not the thermal content | ====> | I have not even the electron envelope. |
| Thermal content exist | <===> | if the electron envelope exist |
| I have no friction I have no viscosity I have no termal content |
<===> | I have no electron envelope |
The high thermal conductivity is caused by loss or partial loss at least of the electron envelope or by its influence suppression.
THE SUPERFLUID COMPONENT and the (high-temperature or low-temperature) PLASMA have something in common with each other. In both cases we have no electron envelope.
22. Superconductivity
The conducting electrons in metals transfer the electric charge and heat well. How it is then possible, that they do not contribute practically to the heat capacity at room temperature? (S. Janos, The Low Temperature Physics, p. 102 - SPN Bratislava, 1979).
The conducting electrons also rotating around their own axes, like the electrons in superfluid or superconductive state.
The electric current is then the flow of conducting electrons ripped out of the valence shells of atoms envelopes rotating around their own axes.
We can gain the high-temperature superconductivity by breaking of the
orbits of electrons increasing their velocity (i. e. by the reduction of
their force reach radii for ![]() and reducing the motion of atoms nuclei (or ions) increasing the volume
for the electrons transition (what is in fact indirectly the decrease of
temperature).
and reducing the motion of atoms nuclei (or ions) increasing the volume
for the electrons transition (what is in fact indirectly the decrease of
temperature).
We will increase the volume for transition of the electrons through maximum solid breaking of orbits of the electrons. This will decrease the "size of atoms" of ~ 105 fm to the "size of nuclei" ~ 1fm i. e. it will decrease (105)3=1015 times (!!!) the "volume of obstacles for electrons". Will not the grid structure of metal disintegrate moreover as in plasma?
Evidently it will be necessary to freeze the nuclei motion in order to keep the grid structure of "superconductor" i. e. to remain the real nuclei of atoms (or ions) in neutral points of grid not to gain a chaotic motion. That can probably only be achieved in strong magnetic fields, or at low temperature. Increasing the speed of electrons to the speed close to the one of light, we decrease the radius of force range of electrons. It means, that for v~c the electrons could perhaps transit also through the nuclei (ions) like through the screen. Then it would no matter whether or not it is the low temperature, or if the conductor grid is kept or not. It is a matter of not disintegrate the "conductor" to plasma or keeping in within the "space of the conductor". The electric current in the circuit of superconductive material flows almost for the infinite time, since it is the motion of free electrons rotating around their axes in almost free medium. There are no atoms in the neutral points of grid, just nuclei or ions and they are almost frozen, i. e. they do not oscillate thermally, chaotically around the equilibrium positions almost at all. They probably just rotate, so their effective cross-section is also small. At the same time the effective cross-section of electrons is smaller, for they move along the circle at the high speed. In which way their radius of force range is also decreased. By the accelerating voltage U=1010 V for electrons and voltage U=1013 V for protons (see fig. 3.8) it should originate superconductivity at room temperature.
23. The wavelength according to Broglie
![]()
according to Compton ![]()
according to Vlček 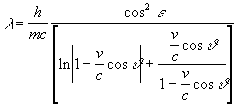
24. The moment of momentum is kept - it is constant (it results from the generalized law of inertia)
| because the moment of inertia is kept in the center-of-mass coordinate system |
but the momentum is not kept in general m1v1 does not equal m2v2
because R1 does not equal R2 the radius of electron and nucleus revolve around, the common center of gravity is different.
Only in a special case e. g. on the Earth surface, when R1=R2=RZ it is valid that m1v1RZ=m2v2RZ
i. e. m1v1=m2v2 (a boat on a water level)
25. The orbit radius ![]()
26. The force range radius - see relations (3.25) to (3.27) and Fig. 3.13. The experimental evidence: a trace of particle in Wilkinson’s chamber. High speed, low density of ionization.
27. From the wavelength of the spectral
line and from its thickness we can even calculate the speed of electron
by its circular motion around nucleus ![]() )
also the radius of orbit Rorbit for all spectral lines.
We just need a spectroscope tables of wave- lengths (
)
also the radius of orbit Rorbit for all spectral lines.
We just need a spectroscope tables of wave- lengths (![]() )
to find out all proportions in atoms.
)
to find out all proportions in atoms.
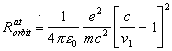 because
because
![]() quasicircle
quasicircle
Substituting
![]()
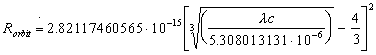
For 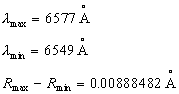
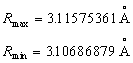
28. The ratio of the mass of two bodies rotating around the common center of gravity e. g. in atom of hydrogen is essential:
![]()
then
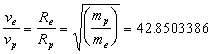
For the solar system in our GALAXY
![]()
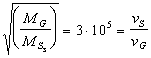
29. The higher the speed of particle, the shorter radius of its own force range (it is significant for v > 0,05c). At the same time it is the explanation of the short radius of force range of the particles of strong fields.
Conversely, the particles in electromagnetic, gravitational and weak
fields have long radius of force range i. e. the particles of these fields
move at low speed of v < 0,05c. We have the effective cross-section
of r = 10-15 m if it is defined that ![]() where r is the radius of force range of the particle for
where r is the radius of force range of the particle for ![]() and
and ![]() up
to 0,06 barn. According to Vanovic the experiment for example gives for
the scattering of
up
to 0,06 barn. According to Vanovic the experiment for example gives for
the scattering of ![]() barn at
barn at ![]() .
.
30. Heisenberg’s uncertainty principle and our theory are in absolute agreement: "The bigger the impulse (i. e. the higher speed, too) the shorter force range radius."
"The smaller the impulse (the slower speed) the longer force range radius."
High speed is accompanied by the short radius of force range. Slow speed is accompanied by the long radius of force range.
|
|