3.3. Nuclear field
3.3. Nuclear field |
|
In nuclear physics, the energy of particles is usually given in units
of eV, MeV, GeV, TeV, ... We get it from the product of unit charge of
electron 1e and the accelerating voltage U (V). Taking into consideration
that this is the movement of charges at the speeds of 
,
we have re-calculate the currently given energies of particles 
with regard to real energies of particles given in equation
 |
(3.14) |
There the real speed v1 is taken for which it holds
 |
(3.15) |
or
 |
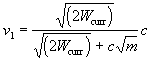(3.16) |
respectively. Let us derive the relations. For the classical speed
 |
(3.17) |
m - mass of particle
e - charge of particle
KIRCHNER (1932) and DUNNINGTON (1933) found out that the relation (3.17)
does not hold for classical velocities comparable with the speed of light
(for high voltages). Now it is known that for the charge moving at the
speed of 
we must take
 |
(3.18) |
instead of 
.
The equation (3.18) is analogical to the equation (2.20).
The real speed of the charged particle then is
 |
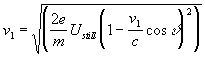(3.19) |
from which we get the relations (3.15) or (3.16)
respectively.
(
, velocity
is only in the direction of motion)
Graphic dependence of 
on U[V] for the electron (me) and proton (mp)
is shown in fig. 3.8.
The comparison of the "standstill" energy of the particle
W of the proton mass (mp) or electron mass (me)
respectively with the energy so far recognized is given in fig.
3.9. The dependence of the "standstill" (Einstein’s terminology)
energy of the particle W on 
.
is represented, similarly as the intensity of the electric field, by Pascal’s
screw stocks, analogy of figs. 2.7.-2.10.
It is necessary to distinguish
the kinetic energy of the particle Tkin according to
equation (3.11) from the "standstill" energy
of the particle W according to equation (3.14)
and the total energy of the particle
 |
(3.20) |
Total energy of the particle TT corresponds to the total energy defined by Einstein
 |
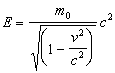(3.21) |
while W according to (3.14) corresponds to
 |
(3.22) |
The difference between the total energy as defined by Einstein (3.21) and Wcurr according to (3.22) equals the difference between TT according to (3.20) and W according to (3.14).
The dependence of Tkin on Wcurr is shown in fig. 3.10.
The dependence of Tkin on ,
W on ,
and
on is shown
in fig. 3.11.
|
|
