2. THEORY AND ITS COMPARISON WITH EXPERIMENT |
|
Let us have a system of coordinates (x, y, z) connected with the medium causing propagation of light. Let the electric field intensity in this medium propagate at speed c in all directions. It is known from Coulomb's law that intensity of the still standing charge in relation to the system of coordinates (x, y, z) decreases with the square of distance from that charge then represented by hyperboles symmetrical to the charge, illustrated in section as follows:
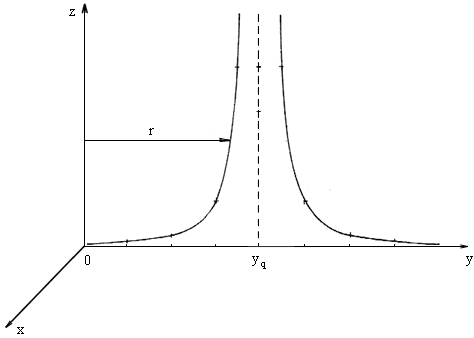
Fig. 2.1. The intensity of the stillstanding charge
r - distance of the hyperbole point from the beginning
Charge q is situated at level yz and in the distance of yq from the beginning in the direction of axis y.
Let us now examine what would happen with the form of curves representing the intensity of the electric field, if charge q will move in a uniform straight line motion in the direction of the axis y at a constant speed v. Let's thus join firmly the system of coordinates (x', y', z') with the charge q, see fig. 2.2.
r - distance of the hyperbole point from the beginning
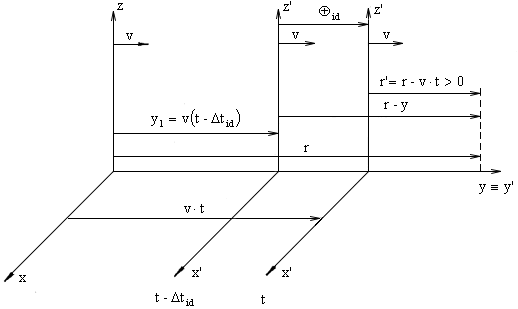
Fig. 2.2. The system of coordinates (x', y', z')
Distance r' is measured in direction of axis y' from the charge (or from the beginning O' respectively), while it is valid
| r'=r-vt | (2.1) |
At the moment t0=0 both systems become identical.
When ![]() , the charge finding itself at the distance of
, the charge finding itself at the distance of
![]() would emit intensity propagating at speed c,
which at the moment of t would come to point r in time of
would emit intensity propagating at speed c,
which at the moment of t would come to point r in time of
| (2.2) |
| (2.3) |
The index id means that is the case of propagation of the electric field intensity in direction of the charge motion.
Let the ![]() be the distance between the
position of the charge at the moment of
be the distance between the
position of the charge at the moment of ![]() (i.e. when the charge has emitted the intensity to point r) and position of the charge at the
moment t, when the intensity emitted "has reached" the point r.
(i.e. when the charge has emitted the intensity to point r) and position of the charge at the
moment t, when the intensity emitted "has reached" the point r.
At the time of ![]() the charge will cover the distance of
the charge will cover the distance of
| (2.4) |
This is the distance at which the charge "outrun" the intensity propagated in direction
of the charge motion. Consequently the intensity of the moving charge in relation to the system
of coordinates (x, y, z) will change its form in the respective
![]() of various r:
it will be deformed (see fig. 2.3)
of various r:
it will be deformed (see fig. 2.3)
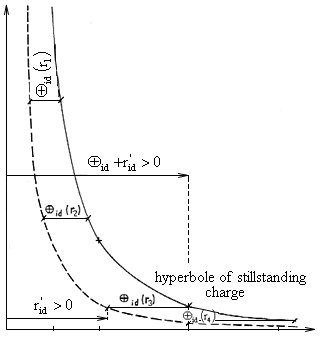
Fig. 2.3. The intensity of the moving charge in the direction of the motion ![]()
It is evident that with increasing distance ri (i = 1,2,3,...)
the respective "retardation of intensity" ![]() (ri)
also increases, as can be seen in equation (2.4.). As the intensity of the moving charge in the direction
of the motion
(ri)
also increases, as can be seen in equation (2.4.). As the intensity of the moving charge in the direction
of the motion ![]() at point r' and moment t
equals the intensity of the stillstanding charge at point
at point r' and moment t
equals the intensity of the stillstanding charge at point ![]() at the moment of intensity emittance
at the moment of intensity emittance ![]() , then:
, then:
| (2.5) |
| (2.6) | |
| (2.7) |
r are distances of points of hyperbola from the beginning of the non-dashed system,
r' are distances of points of hyperbola from the beginning 0' in a dashed system,
r, r' are variables of the same function ![]() (represented by hyperbolas). In other words, there is distance r, that numerically equals
(represented by hyperbolas). In other words, there is distance r, that numerically equals
![]() distance. Such distance r' numerically
equals
distance. Such distance r' numerically
equals ![]() distance, both being variables
of the same function
distance, both being variables
of the same function ![]() . For detail refer to
(2.6) and (2.7). The issue concerns the same Coulomb's law.
. For detail refer to
(2.6) and (2.7). The issue concerns the same Coulomb's law.
By substituing of (2.5) and (2.4) we get
| (2.8) |
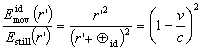 |
(2.9) |
| (2.10) |
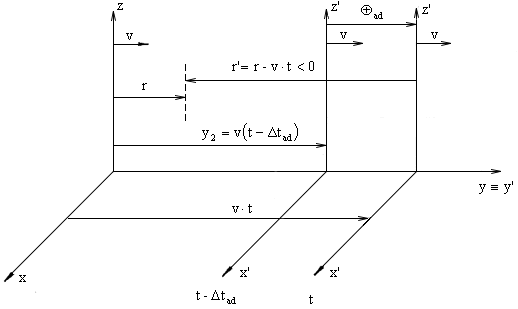
Fig. 2.4. The distance ![]()
The charge moving at the speed of v parallel to the axis y is situated (at the moment t) in the distance of v.t from the axis z.
At the moment ![]() the charge, situated
in the distance of
the charge, situated
in the distance of ![]() will emit the
intensity to the point r.
will emit the
intensity to the point r.
This intensity will reach at the moment t just the point r in time of
| (2.11) |
| (2.12) |
The charge will cover the distance
| (2.13) |
at time ![]() , while r'<0 and
, while r'<0 and
![]() .
.
This is the distance by which the intensity that propagates in the direction opposite to the movement of the charge, is shifted against the intensity of the stillstanding charge in the direction away from the charge, see fig. 2.5.
Analogically to equations (2.5)-(2.10) we achieve the following:
| (2.14) | |
| (2.15) | |
| (2.16) | |
| (2.17) | |
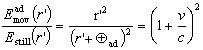 |
(2.18) |
| (2.19) |
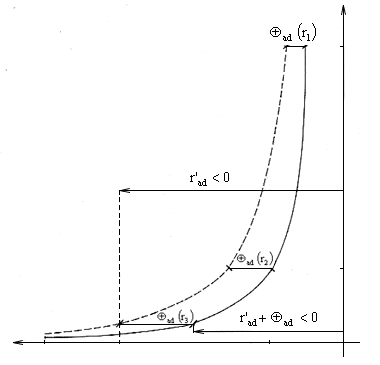
Fig. 2.5. The intensity of the electric field by means of the moving charge against the direction of motion Ead
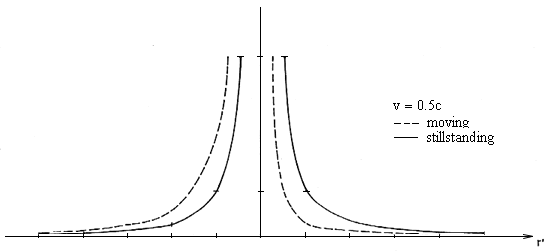
Fig. 2.6. The form of intensity for v = 0.5c
The equations (2.10) and (2.19) are placeable by common equation
| (2.20) |
At level xy, the section of the intensity hyperboloid is, for the stillstanding charge,
the circle with its centre in the charge, for the moving charge it is the case of all types of Pascal's
screw stocks with the charge at the beginning of the coordinates, see figs. 2.7,
2.8, 2.9 and 2.10.
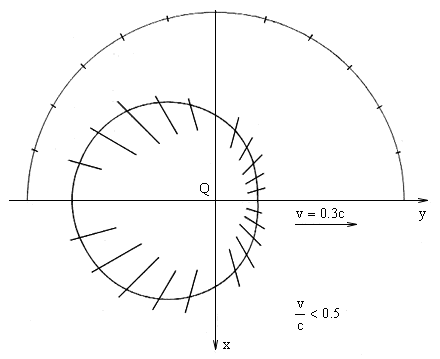

Fig. 2.7, 2.8. At level (x, y) section of the "hyperoloid" of the intensity for various speeds of the moving charge have a shape of all types of Pascal's screw stocks with charge at the beginning of the coordinates
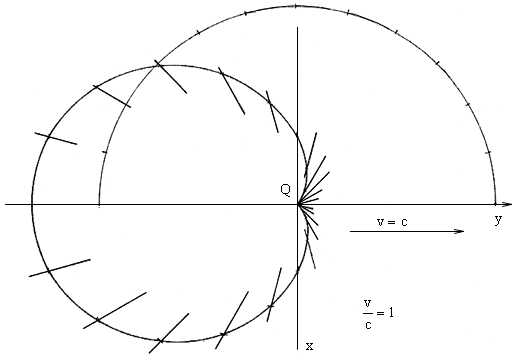
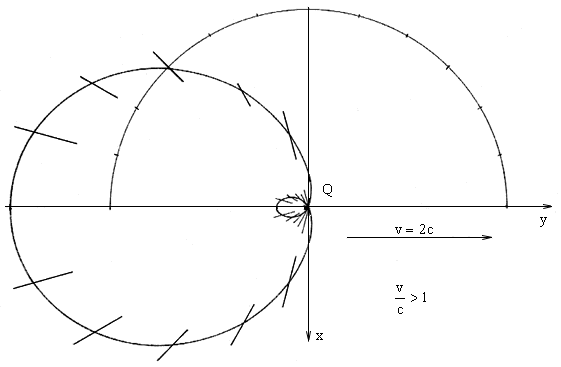
Fig. 2.9, 2.10. At level (x, y) section of the "hyperoloid" of the intensity for various speeds of the moving charge have a shape of all types of Pascal's screw stocks with charge at the beginning of the coordinates
In the period from 1901 to 1906, Kaufmann wrote a number of works, the most coherent of them seems to be(1): concerning experimental evidence of "the changeability of mass with speed". We shall revalue his experiment and will prove - on the basis of the theory given in the preceeding section 2.1.1 - the subject is the influence of intensity of the moving charge on the magnitude of the deviation of influence of intensity of the moving charge on the magnitude of the deviation of beta-rays in the crossed electromagnetic field, and not the changeability of mass with speed.
The attempt is done through a short correct description for sake of qualitative examination of the experiment, utilising some of the measured and calculated values given by Kaufmann in (1).
Beta-rays from Ra source, moving at speed ![]() are simultaneously deflected in the crossed electric and magnetic field, see diagram in fig. 2.11.
are simultaneously deflected in the crossed electric and magnetic field, see diagram in fig. 2.11.
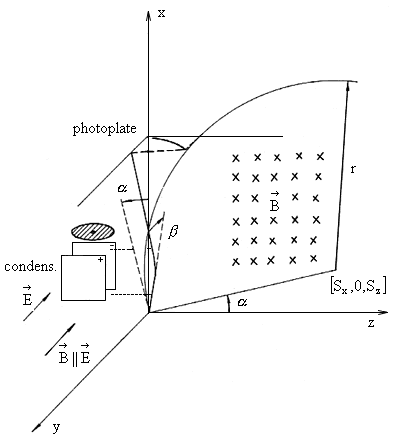
Fig. 2.11. Kaufmann's Experiment - diagram
The device is situated in the evacuated glass vessel. The rays go out from the Ra source, pass the electric screen and create a small spot on a photographic plate.
When the electric field will be created on the condenser plates PP', the additional stripe in the y-
direction will arise apart from the non-diverting middle spot close to 0 (consisting of gamma and little diverting
![]() ).
).
When the entire device is situated between the poles of the U-shaped magnet (with the electric field switched off), the stripe will arise in the direction of the axis z.
While at the magnetic field we have the movement of electrons along circles expressed in the following equations
| (2.21*) |
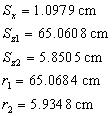
in the electric field we first have the movement along straight line
| (2.22*) |
| (2.23*) |
| (2.24*) |
The values E used in the calculations
| (2.25*) |
Considering out theory on ![]() and the values
(2.25*) be multiplied by
and the values
(2.25*) be multiplied by ![]() we achieve deviations identical with the results of Kaufmann's experiment, see table 1. Thus the theory
under 2.1.1 concerning the intensity of the moving charge of the electric field may
be regarded experimentally confirmed.
we achieve deviations identical with the results of Kaufmann's experiment, see table 1. Thus the theory
under 2.1.1 concerning the intensity of the moving charge of the electric field may
be regarded experimentally confirmed.
| 1631 V | 2603 V | 3250 V | |
| yb[cm] | 0.1236 0.1119 |
0.1493 0.1302 |
0.1664 0.1616 |
| y[cm] | 0.23626 | 0.3873 | 0.4985 |
| yT[cm] | 0.0629 | 0.09947 | 0.12557 |
| yT-theoretical value (our new theory): |
|||
(1)Annalen der Physik, Vierte Folge, Band 19, Leipzig 1906, Verlag von Johann Ambrosius Barth, page 487-552
Let us take the equation (2.20) in the vector form:
| (2.21) |
The force acting on the moving electric charge is
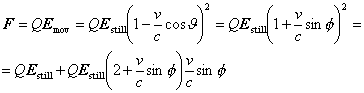 |
(2.22) |
It is known, in line with the classical theory, that a magnetic field is created by the moving charges and electric currents. The result is that the moving charge creates its own magnetic field of induction Bq. It continues in this field in motion. According to Lorentz, the force acting on the moving charge in the electromagnetic field at speed v in the magnetic field of induction B and in the electric field of the following intensity E it is valid:
| (2.23) |
Intensity E of the electric field according to Lorentz equals to our intensity Estill.
As the forces acting on the acting on the moving charge are equal, it must be valid
| (2.24) |
![]()
i.e.
| (2.25) |
while the vectorial equation is in force
| (2.26) |
| (2.27) |
Based on (2.27), Maxwell's equations which are always valid (not only in static) acquire the form:
1.
| (...Gauss law) | ||
| as | ||
| 2. | ||
| there are no magnetic charges | ||
![]()
As in the statics ![]()
further ![]()
We use (2.29) and except of constant it is valid
| (2.31) |
| (...Faraday's law) | (2.32) |
| (2.33) |
Total magnetic field
| (2.34) |
| (2.35) |
On the own magnetic field BQ of the charge moving at speed v it is possible to write:
| (2.36) |
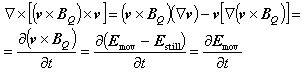
because (2.29),(2.31) and (2.27) are valid and because
| (2.37) | ||
| i.e. | (2.38) | |
Let's accept the following designation
![]()
The equation (2.27) can be written in the following form:
| (2.39) |
where Hstat is the intensity of the static magnetic field and
corresponding angles ![]() relate to angles
relate to angles ![]() .
.
![]()
while ![]()
i.e. ![]()
| or | respectively | (2.40) |
| we get | (2.41) | |
| as | (2.42) | |
| Then | (2.43) |
| Where from | (2.44) | |
| It is possible to write the equation (2.38) also in the following form: | ||
| (2.45) | ||
|
|