3.2. Calculation of the kinetic energy of a body moving at the velocity of v

Let us consider the physical processes in which kinetic energy is transformed into potential one and potential energy is transformed into kinetic one. There is a state in which the potential energy equals total energy of the body (while the kinetic energy equals zero) and the state in which kinetic energy equals the total energy of the body (while the potential energy equals zero). These extreme will help us to calculate the kinetic energy of body. For the potential energy we have

(3.9)

By integrating and utilizing of the relation (3.1) we have

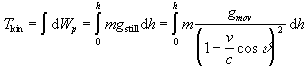
By substituting ,

we get

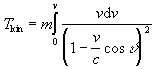(3.10)

Solving by substitution

we get

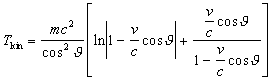(3.11)

while isn’t ,

For we have the kinetic energy in the direction of motion

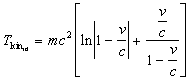(3.12)

For we have the kinetic energy against the direction of motion

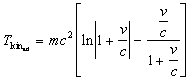(3.13)

If (i.e. v<<c)

utilizing the series

the equations (3.12) and (3.13) will be changed in the equation

Table 5.

x = v/c				A. Einstein
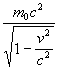0.1	0.00439mc2	0.0057mc2	0.0050mc2	1.005m0c2
0.2	0.0156mc2	0.0268mc2	0.0212mc2	1.020m0c2
0.3	0.0316mc2	0.0719mc2	0.0517mc2	1.048m0c2
0.4	0.0508mc2	0.1558mc2	0.1033mc2	1.091m0c2
0.5	0.0722mc2	0.3068mc2	0.1895mc2	1.155m0c2
0.6	0.0950mc2	0.5837mc2	0.3393mc2	1.250m0c2
0.7	0.1174mc2	1.1293mc2	0.6233mc2	1.401m0c2
0.8	0.1434mc2	2.3905mc2	1.2669mc2	1.667m0c2
0.9	0.1680mc2	6.6974mc2	3.4327mc2	2.293m0c2
0.99	0.1906mc2	94.3948mc2	47.294mc2	7.920m0c2
1.0	0.1931mc2

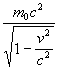complying with the Newton’s mechanics. In Table 5 the values of the kinetic energy are , as well as the total energy according to Einstein . for the speeds of 0.1c to c.