THE NEW COORDINATE SYSTEMS IN PHYSICS
THE NEW COORDINATE SYSTEMS IN PHYSICS |
|
Take the minimal number of identical particles with a globe-like form and forming the nearest organized
configuration. This configuration is a disfenoid at the vertices with four particles (the 
- particle has 4 nucleons). The origin of our new coordinate system is put into the center of gravity of the configuration. This origin
and the centres of the particles determine the semi-lines-semi-axes of the coordinate system. This coordinate system divides the space into four quartespaces.
The pairs of semi-lines (s,t), (s,u), (s,v), (t, u), (t,v), (u,v) determine angles
For angle it precisely holds:
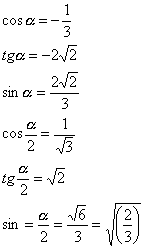
To imagine better the coordinate system (s,t,u,v), we can use the cube. The centre of the cube is the center of gravity of the disfenoid and also the origin of the coordinate system (see fig. 1).
In order to facilitate the transformation to the cartesian coordinate system, this will be somewhat re-arranged:
semi-axes x,y,z will have the same marks, semi-axes (-x),(-y),(-z) will be marked
and so cartesian coordinate system (x,y,z) in the new marking will be revealed as a system
(
) formed by semi-axes .
These, regarding to the coordinate system (s,t,u,v), will be determined as follows:
semi-axis x is the symmetral of the angle (see fig. 2)
semi-axis y is the symmetral of the angle in
" - plane" (t,u)
semi-axis z is the symmetral of the angle in
" - plane" (u,v)
semi-axis 
is the symmetral of the angle in
" - plane" (t,v)
semi-axis 
is the symmetral of the angle in
" - plane" (s,v)
semi-axis 
is the symmetral of the angle in
" - plane" (s,t).
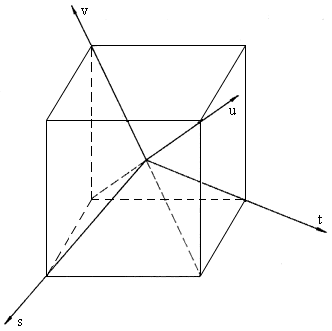
Fig. 1. The coordinate system (s,t,u,v)
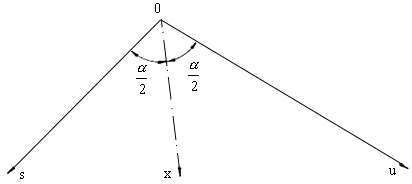
Fig. 2. The semi - axis x is the symmetral of the angle
After drawing both coordinate system we will achieve fig. 3.
The cartesian coordinate system divides the space into 8 octants:
.
The trinities of " - planes" determine four equal quarter-spaces: (s,t,u), (s,t,v), (s,u,v), (t,u,v).
It is impossible to divide the space into equal parts using less than 4 semi-axes. It means that these quarter-spaces are the largest possible parts of the space formed
by the minimal number of semi-axes.
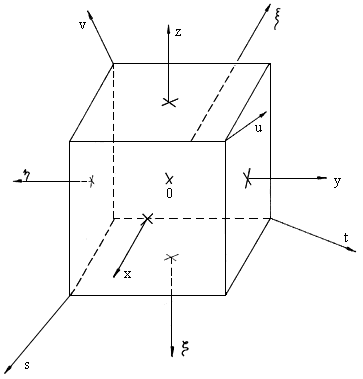
Fig. 3. Both coordinate system (s,t,u,v) and ()
The values of coordinates will be read in two ways:
a) The straight lines placed from an arbitrary point parallel to the axes s,t,u,v determine coordinates s,t,u,v, fig. 4.
Zero in the contained coordinate means that the point is placed in the quarter space determined by coordinates other than zero.
See the following transformation equation between (s,t,u,v) and ():
(s,t,u)
(s,u,v)
(s,t,v)
(t,u,v)
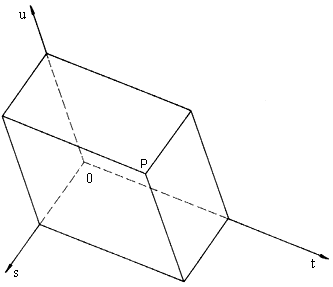
Fig. 4. The coordinates (s,t,u,v)
| (s,t,u): | (s,u,v): | ||
 |
 | ||
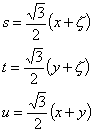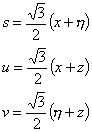| (s,t,v): | (t,u,v): | ||
 |
 |
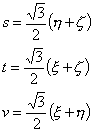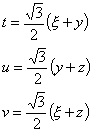The distance between two points (s1,t1,u1,v1) and (s2,t2,u2,v2) is determined as follows:
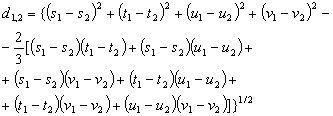
b) The planes placed from an arbitrary point perpendicular to the axis s,t,u,v determine coordinates s*,t*,u*,v*, see fig. 5.
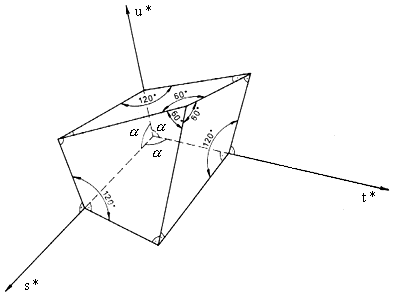
Fig. 5. The coordinates s*,t*,u*,v*
See the following transformation equations between s*,t*,u*,v*, and
:
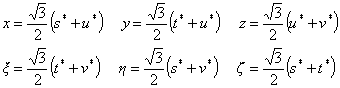
| (s*,t*,u*): | (s*,u*,v*): | ||
 |
 | ||
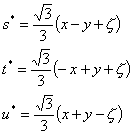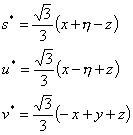| (s*,t*,v*): | (t*,u*,v*): | ||
 |
 |
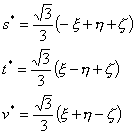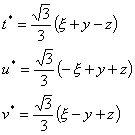Quadrate of distance between two points (s1*,t1*, u1*,v1*) and (s2*,t2*, u2*,v2*) is determined by this equation:
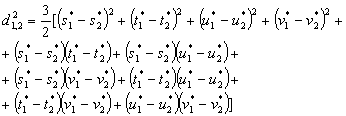
See the following transformation equation between (s,t,u,v) and (s*,t*,u*,v*):
| (s,t,u): | (s,t,v): | ||
 |
 | ||
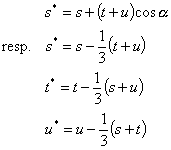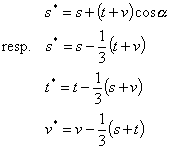| (s,u,v): | (t,u,v): | ||
 |
 | ||
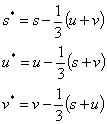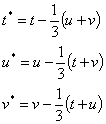| (s,t,u): | (s,t,v): | ||
 |
 | ||
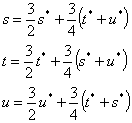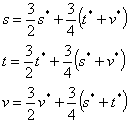| (s,u,v): | (t,u,v): | ||
 |
 |
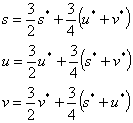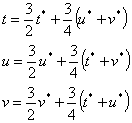Rotation around axis x,y,z - the angle of rotation is 
- are invariant. They perform the disfenoid into equivalent positions. The rotations around the axis s,t,u,v - the
angle of rotation is 
- are the invariant ones.
E,s,s-1,t,t-1,x,u,u-1,y,v,v-1,z form the group of rotation,
see Tab. 1.
columns - Acts as the first, rows - Acts as the second
| E | s | s-1 | t | t-1 | u | u-1 | v | v-1 | x | y | z | |
| E | E | s | s-1 | t | t-1 | u | u-1 | v | v-1 | x | y | z |
| s-1 | s-1 | E | s | z | u | y | v | x | t | u-1 | t-1 | v-1 |
| s | s | s-1 | E | v-1 | y | t-1 | x | u-1 | z | v | u | t |
| t-1 | t-1 | z | v | E | t | x | s | y | u | v-1 | s-1 | u-1 |
| t | t | u-1 | y | t-1 | E | v-1 | z | s-1 | x | u | v | s |
| u-1 | u-1 | y | t | x | v | E | u | z | s | s-1 | v-1 | t-1 |
| u | u | v-1 | x | s-1 | z | u-1 | E | t-1 | y | t | s | v |
| v-1 | v-1 | x | u | y | s | z | t | E | v | t-1 | u-1 | s-1 |
| v | v | t-1 | z | u-1 | x | s-1 | y | v-1 | E | s | t | u |
| x | x | u | v-1 | v | u-1 | s | t-1 | t | s-1 | E | z | y |
| y | y | t | u-1 | s | v-1 | v | s-1 | u | t-1 | z | E | x |
| z | z | v | t-1 | u | s-1 | t | v-1 | s | u-1 | y | x | E |
A nucleus, whose constituent nucleons are arranged to occupy the least possible sphere, is said to have a close-packed structure. Close-packed structures occur when the bonding forces are spherically symmetric. If the force between two nucleons is f, then total force impacting each nucleon in disfenoid and aiming into center of mass of disfenoid is 2.449 f. The total force on each nucleon impacting two interleaved disfenoids (i.e. into cube) is 3.2896 f, i.e. bigger than by disfenoid. Therefore by two interleaved disfenoids each nucleon is attracted into center of mass of cube by greater force as into center of mass of disfenoid.
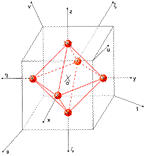
Fig. 6. Sphere 6 |
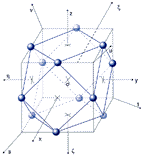
Fig. 7. Sphere 12 |
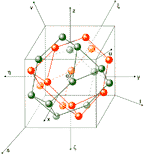
Fig. 8. Sphere 24 |
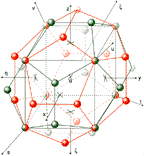
Fig. 9. Sphere 32 |
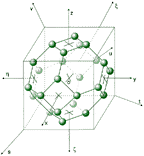
Fig. 10. Sphere 24 which with sphere 24 from fig. 8 give sphere 48 |
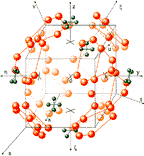
Fig. 11. Sphere 96 |
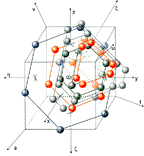
Fig. 12. Nucleons by axis u from all spheres 6, 8, 12, 24, 32, 48, 96
|
Similarly it is at shell 12 (see fig. 7) also at shell 24 see fig. 8 (two interleaved disfenoids + and - in which nucleons are 1/3 and 2/3 of the length of the diagonals of any face of cube). The advantage of the new coordinate systems (s,t,u,v) and (s*,t*,u*,v*) is that the nucleons in nuclei can be on axes s,t,u,v respectively at perpendicular level to these axes, while axes s,t,u,v pass through center of mass 3 or 6 neighbouring nucleons see fig. 12.
By the combination of the cartesian coordinate system with our new coordinates arise a very firm fastening
structure for description of nuclear spheres (shells, subshells). All nucleons from shells can be on sphere
and simultaneously on axes see fig. 6
- red dipyramid 6 nucleons, respectively on axes s,t,u,v - cube 8 nucleons see fig. 5,
(coordinate see Table 2), respectively in the middle of each edge of cube-blue sphere 12 nucleons,
respectively in 1/3 and 2/3 of the length of the diagonals of any face of cube (see fig. 8)
sphere 24 nucleons while axes s,t,u,v pass through centres of mass 3 or 6 nucleons, respectively
fig. 9 shows sphere 32 nucleons (two interleaved pentagonal dodecaeders + and -), in
fig. 10 shows sphere 24 which, with sphere 24 from fig. 8, gives sphere 48
nucleons, and in fig. 11 is sphere 96 nucleons (two interleaved pentagonal and hexagonal 32-eders)
whereby axes s,t,u,v pass through centres of mass 3 and 6 neighbouring nucleons situated in the mutually
parallel and perpendicular level to these axes. Respectively, axes
pass through center of mass 4 neighbouring nucleons at perpendicular level to these axes -
see fig. 11. Two interleaved spheres 8 and 12 give us sphere 20 - the magical number.
Four interleaved spheres 6,12,24 and 8 give us sphere 50 - magical number. Four interleaved spheres 8,24,24 and 96 give us sphere 152 - magical number. Three interleaved spheres 6,24 and 96 give us sphere 126 - magical number. Five interleaved spheres 6,8,12,24 and 32 give us sphere 82 - magical number. If it is assumed that the nucleons in an elementar spherical nucleus are spheres in contact, it is easy to calculate their radii of force reach from a knowledge of the spherical nucleus structure and the sphere parameters. The latter information can be obtained by "gamma" ray diffraction analysis.
| Sphere 6: | ||
|
(s,t,u,v) | (s*,t*,u*,v*) |
| (a,0,0,0,0,0) |  |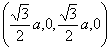
 |
| (0,a,0,0,0,0) |  |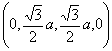
 |
| (0,0,a,0,0,0) |  |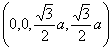
 |
| etc. | ||
| Sphere 8: | ||
| (a,0,0,0,a,a) |  |
 |
| (0,a,0,a,0,a) |  |
 |
| (a,a,a,0,0,0) |  |
 |
| etc. | ||
| Sphere 12: | ||
| (a,a,0,0,0,0) |  |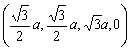
 |
| (a,0,a,0,0,0) |  |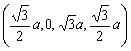
|
| (0,a,a,0,0,0) |  |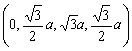
|
| etc. | ||
| Sphere 24: | ||
 |
 |
 |
 |
 |
 |
 |
 |
 |
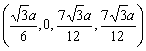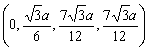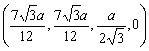| etc. | ||
|
|