2.3. Doppler's principle - correct relations

In one second a standing source will emit n oscillations of the wavelength

c - the speed of light in the standing medium

During the time of

, the oscillations will be distributed in the distance of

When the source moves away from the observer at speed u the oscillations would "expand" in the distance of

a) When the source approaches to the observer at speed u (sign-u), the oscillations would be compressed in the distance of

Let the observer move against the oscillation at speed v (sign-v).

During the period

, the oscillations would be compressed in the distance of

From which

The frequency would thus be heightened from n to N and it is valid

From which

(2.50)

This is the case of

b) If they both (S and O) move away with regard to the medium, i.e. the case is +v and +u. We get "the expansion" of the wave length both by the source and observer. That is why

from which

(2.51)

c) The case when the source is "expanding" the wavelength (+u) and the observer is "compressing" it (-v)

Where from

(2.52)

d) The source is "compressing" the wavelength (-u) the observer is "expanding" is (+v).

(2.53)

Through combination of the equations (2.50) through (2.53) we get

(2.54)

Generally

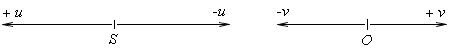
(2.55)

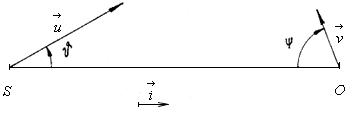
Fig. 2.22. Doppler's principle - generally

Fig. 2.23. The transversal Doppler's phenomenon - incorrectly interpreted

see fig. 2.22. (2.55) can be transcribed as

(2.56)

where w is the relative speed in direction of connecting line SO. i is the unit vector in direction of the connecting line SO, beginning at S.

The transversal Doppler's phenomenon is incorrectly interpreted in the existing theories - see fig. 2.23.

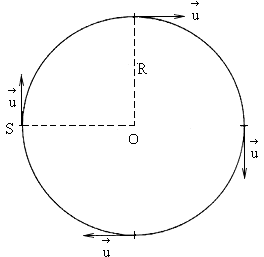
Fig. 2.24. The source (S) motion along the circle with the observer (O)

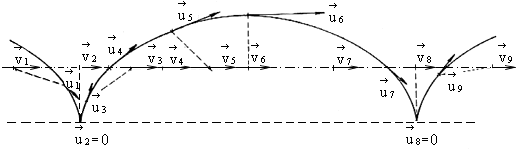
Fig. 2.25. Alternately accelerated and decelerated motion along a normal cycloid

The angle between the connecting ine SO(i_k) and the direction of motion S(u) is permanently changing in range from several degrees up to . The pure transversal Doppler's phenomenon should occur with the constant angle of , i.e. the source motion along the circle with the observer in its centre (see fig. 2.24). Alternately, accelerated and decelerated motion can occur, along a normal cycloid where it always holds that so that the source speed is not decisive, while is valid,

(see fig. 2.25)

It is possible to materialize this case in such a way that the source will be fastened on the circumference of the circle, the observer will be placed in its centre, while the circle will roll along the straight line and the centre of circle (the observer) will move at speed v.

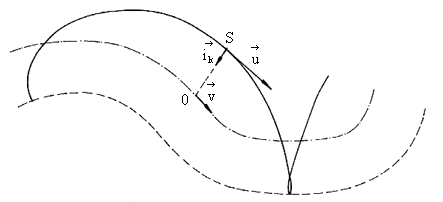
Fig. 2.26. The transversal Doppler's phenomenon - general

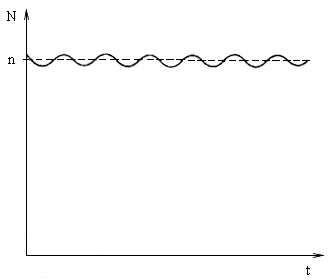
Fig. 2.27. The frequency N - as perceived by the observer, "pulsates" around the source frequency n

Analogically, if S (source) and O (observer) are interchanged, then it holds

Should any such circle roll along any curve (with the source on its circumference and the observer in its centre), the result would be the generally known case pictured in fig. 2.26 and it holds

Analogically, if S and O are interchanged, then it holds

In this way the change of frequency N occurs permanently. The frequency N as perceived by the observer - "pulsates" around the frequency of source n, see fig. 2.27.