3. CONSEQUENCES 1 |
|
For the sake of simplicity let us consider for instance the gravitational field of the Earth. Analogically to (2.20), for the intensity of the gravitational field one could write:
| (3.1) |
Should we want to withdraw from the gravitational field of the Earth,
it will be necessary to aim at ![]() .
.
Then the weight of bodies will be falling down ![]() .
.
However, the mass of bodies remains unchanged. Individual material particles
of the body will move in a prevailing measure in direction to the Earth
at the highest possible speed (in ideal case ![]() ),
but the center of gravity should at the same time move away from the Earth.
This is possible only with the special rotation of body around the axis
passing trough the center of gravity, while the body rotates at vertical
level (see fig. 3.1).
),
but the center of gravity should at the same time move away from the Earth.
This is possible only with the special rotation of body around the axis
passing trough the center of gravity, while the body rotates at vertical
level (see fig. 3.1).
c - the speed and direction of propagation of the gravitational
waves of the Earth. The points moving at speed of c towards the
Earth (![]() )
are of no weight. The points moving at the speed of c away from the Earth
weight 4x more than is standstill (see fig. 3.2).
)
are of no weight. The points moving at the speed of c away from the Earth
weight 4x more than is standstill (see fig. 3.2).
In consequence of rotation, the center of gravity will be shifted to the part departing from the Earth. This means that the body should depart from the Earth as a consequence of rotation (since the shifted center of gravity is situated in the half emerging during the rotation, i. e. departing from the Earth).
For the sake of simplicity, let us consider the rotating body whose mass is evenly distributed on the circle with radius r.
In case such a body does not rotate, its center of gravity is in the
center. Once it starts rotating at the circumference speed of v,
the center of gravity will be shifted in the distance of rc,
which will be calculated as in fig. 3.3. Each point
of weight G0 will, in result of rotation, weight ![]()
There is a certain angle ![]() for which
for which
| (3.2) |
The weight of points to the right from Cmov must be equal to the weight of points to the left from Cmov which will be written as follows:
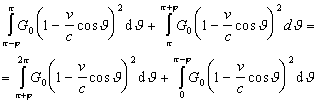 |
(3.3) |
Where from
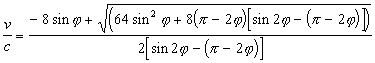 |
(3.4) |
Substituting for ![]() we get the Table 2 which represents the dependency of
we get the Table 2 which represents the dependency of ![]() on
on ![]() , see
fig. 3.4.
, see
fig. 3.4.
80 60 40 37 36 32.123 |
0.1736 0.5 0.7660 0.7986 0.8090 0.847 |
0.0886197118 0.30472815857 0.765471182633 0.927252176745 1.00053925635 1.89550406058 |
Two forces act on shifted center of gravity
a) gravitational force of the Earth = the weight of body
b) the accelerated rotation of body upwards.
Note:
| (3.5) |
For ![]()
In order to compensate the weight of body we must have the accelerated rotation. Let the angle acceleration be
| (3.6) |
Then with the accelerated rotation is ![]()
![]()
Immediate acceleration of the shifted center of gravity will be calculated as follows:
| (3.7) |
at - tangential, rotational acceleration
an - normal, centripetal acceleration which is compensated by
stiffness of system, by rigidity of the rotation axis.
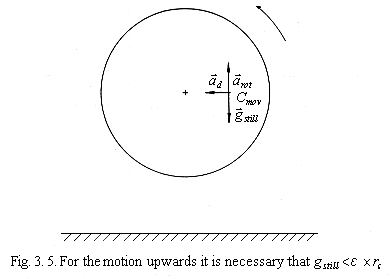
For the motion upwards it is necessary that
| (3.8) |
see fig. 3.5.
The periods are calculated in Table 3, in which the circle points will reach the relevant circumferential speed for various values of the angle accelerations.
| v = 10-4c | t = 3.104s | t = 3.103s | t = 3.102s | t = 30s | t = 3s |
| v = 10-3c | 3.105s | 3.104s | 3.103s | 300s | 30s |
| v = 10-2c | 3.106s | 3.105s | 3.104s | 3.103s | 300s |
| v = 0.1c | 3.107s | 3.106s | 3.105s | 3.104s | 3.103s |
| v = c | 3.108s | 3.107s | 3.106s | 3.105s | 3.104s |
| r = 1m | r = 10m | r = 100m | |
| v = c | rc = 0.8m | rc = 8m | rc = 80m |
| v = 0.1c | rc = 0.2m | rc = 2m | rc = 20m |
| v = 0.01c | rc = 0.018m | rc = 0.18m | rc = 1.8m |
| v = 0.001c | rc ~ 0.0014m | rc ~ 0.014m | rc ~ 0.14m |
Values rc are calculated in Table 4 for various r
and ![]()
Several examples: ![]()
i.e. at the acceleration of 103 rev / s2 and the circle diameter of 20 m, "the circle" should get off the Earth in less than five minutes. At the acceleration of 100 rev / s2 and diameter of 20 m, the circle should get off the Earth in less than 50 minutes.
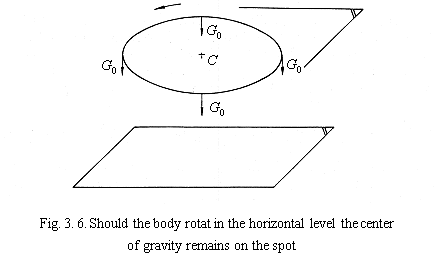
At the acceleration 105 revolutions / s2 and diameter of 20 m the "circle" of mass points should get off the Earth in less than 3 sec. Other values for diameters, accelerations may be acquired by using the Tables 2, 3, 4. For the sake of comparison, "Auswuchtzentrum mit Vakuumkessel", Schenck, FRG, reaches maximum 30 000 revol./min.= 500 revolutions/sec with the rotor diameter of 900 mm. Should the body rotate in the horizontal level (i. e.the level parallel to the Earth), the center of gravity remains on the spot (fig. 3.6).
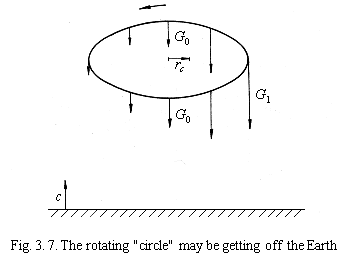
Any inclination of the circle from the horizontal level when projected at the vertical level results in ellipse. The shift of center of gravity increases in line with the inclination of the Ącircle" from the horizontal to vertical level. It means that the more the rotating "circle" may be getting off the Earth (see fig. 3.7). Conversely, if we want to stop the getting off the Earth, it is enough to level the "circle" into the horizontal level. It is evident that the highest speed of getting away from the Earth will be achieved in the rotation in vertical level. If the rotation level of the "circle" forms with the horizontal level an angle of 45o, the "circle" acquires the average speed of getting off the Earth i. e. by deceleration of the rotating "circle" needs straightening more in the horizontal level. During acceleration it is necessary to swing out the rotating "circle" so that it rotates closer to the vertical level. The real rotating body will qualitatively behave in a way similar to our "circle".
|
|